Ein Zahlensystem mit der Basis 32? Äh, welche Basis?
Kleiner Ausflug in Wissen das man nicht zu brauchen glaubt und doch jeden Tag nutzt.
Oder: warum in der Matrix Hieroglyphen zu sehen sind.
Einleitung: Dezimalsystem
Was die meisten von uns ja schon wieder aus der Schulzeit vergessen haben: unser Dezimalsystem ist ein Zahlensystem mit der Basis 10. Wir kennen alle noch die Bezeichnung der Stellen (10’er, 100’er, 1000’er, …). Aber wie kommt das zustande? Durch Basis und Exponent im Stellenwertsystem. Die erste Stelle hat den Wert 10⁰. Das ergibt per Definition den Wert 1. Die zweite Stelle hat den Wert 10¹, das ergibt 10. Die dritte Stelle 10² ( = 10*10 = 100 ), die vierte 10³ ( = 10 * 10 * 10 = 1000 ) und immer so weiter. Bei den Nachkommastellen geht es genau so, nur mit negativen Exponenten. Die erste Nachkommastelle mit 10⁻¹ ergibt 0,1. Die zweite mit 10⁻² dann 0,01 und immer so weiter.
Das ergibt den Wert der Stelle. Wie oft dieser Wert zählt wird durch die Zahlzeichen bestimmt (das was wir landläufig Zahlen nennen). In unserem Dezimalsystem sind das die Zeichen 0, 1, 2, 3, 4, 5, 6, 7, 8, und 9. Streng genommen muss man hier nämlich unterscheiden: Die Potenz bestimmt den Wert einer Stelle, die Zeichen bestimmen wie oft die Stelle zählt, und die Summe aller gezählten Stellen ergibt die Zahl. Verwirrend ist das weil 0-9 auch die ersten Zahlen sind. Das sind die Zahlen die sich mit nur einer Stelle im Dezimalsystem darstellen lassen. Für die 10 brauchen wir schon zwei Stellen.
Beispiel:
2111 = (2 * 10³) + (1 * 10²) + (1 * 10¹) + (1 * 10⁰) = 2000 + 100 + 10 + 1 = 2111
So weit so überflüssig könnte man meinen. Ist es aber nicht. Warum sollte man jetzt ein Zahlensystem entwerfen das eine andere Basis als die Zehn hat? Anders gefragt, warum sollte man nicht ein komplett anderes Zahlensystem entwerfen, und warum benutzen wir überhaupt dieses? Ja, es gibt andere. Nicht nur andere Stellenwertsysteme, auch sogenannten Additionssysteme. Die römischen Zahlen zum Beispiel. Wer dazu noch mehr sehen möchte findet dies unter KnowHow: Zahlen.
Herleitung: Base32
Nur so viel sei gesagt: die binären (0 und 1) im Computer sind ein duales Zahlensystem. Und wenn man heutzutage auf einem Computer einen Salat aus Buchstaben und Zahlen sieht, dann handelt es mit hoher Wahrscheinlichkeit um das hexadezimale System. Das nutzt nämlich die Basis 16. Wegen der Basis 16 kann man mit einer Stelle schon die Werte 0-15 abbilden. Um das tun zu können braucht man aber Zeichen, Zahlzeichen, genau wie im dezimalen System. Damit die Menschen sich nicht zu sehr umgewöhnen müssen, hat man dafür folgende verwendet: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Dabei hat das A den Wert 10, B = 11, C = 12, D = 13, E =14 und F = 15. Während die erste Stelle im hexadezimalen System genau wie im dezimalen den Wert 1 hat (wegen 16⁰), hat die zweite Stelle aber schon den Wert 16 (16¹) und die dritte den Wert 256 (16²). Das bedeutet eine „10“ im hexadezimalen System hat den Wert (1 * 16¹) + (0 * 16⁰) = 16. Eine „100“ hat den Wert (1 * 16²) + (0 * 16¹) + (0 * 16⁰) = 256.
Wo der Vorteil liegt? Nun, im hexadezimalen System kann man größere Zahlen mit weniger Stellen abbilden. Im dezimalen kann eine Stelle von 0-9 und zwei Stellen von 0-99. Im hexadezimalen System kann eine Stelle von 0-15 und zwei Stellen können von 0-255. Wenn ich die Zahl 250 darstellen möchte habe ich hexadezimalen also schon eine Stelle gespart. Bei größeren Zahlen entsprechend (exponentiell).
Wenn man jetzt ein System entwirft das mit der Basis 32 arbeitet (nennen wir es „unser 32’er“), hat man den Vorteil noch einmal erhöht. Dann kann die erste Stelle schon von 0-31 und zwei Stellen können von 0-1023. Also wenn ich eine 1020 darstellen möchte habe ich schon zwei Stellen gespart. Für die Zahlzeichen nutze ich einfach wieder das Alphabet: die Buchstaben A – V mit den Werten 10 – 31. Eine 100 wäre dann (1 * 32²) + (0 * 32¹) + (0 * 32⁰) = 1024 + 0 + 0 = 1024. Eine 10 wäre (1 * 32¹) + (0 * 32⁰) = 32 und eine 1V wäre (1 * 32¹) + (31 * 32⁰) = 32 + 31 = 63. Cool? Irgendwie schon ein bisschen, aber das beste kommt noch.
Ausblick: Hieroglyphen und Aliens
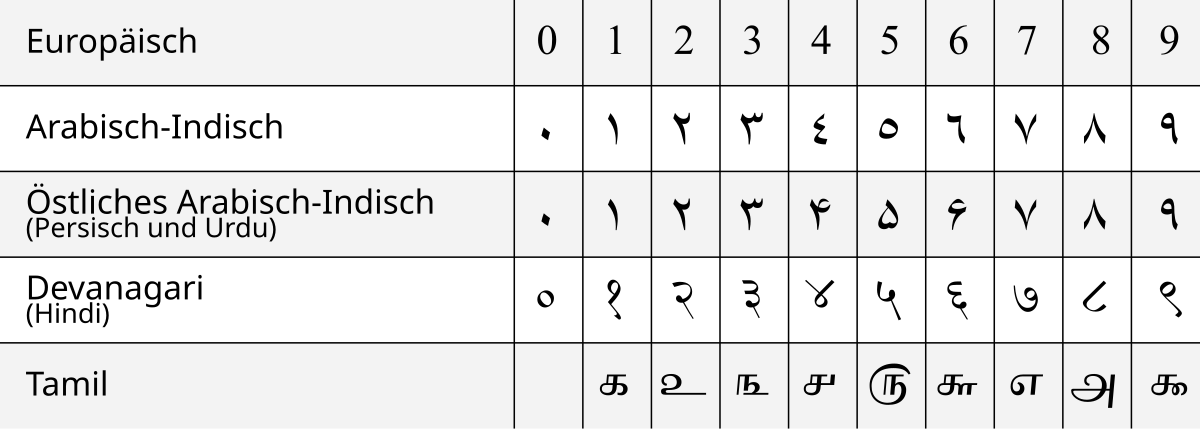
Und genau hier kommt der Haken mit dem Clou ins Spiel: rein theoretisch kann ich beliebige Zeichen für die Zahlzeichen verwenden. Ich könnte genau so gut alt-germanische Runen für die Zahlzeichen nehmen. Im alten Futhark gibt es immerhin 24 Stück, also kann ich statt A – V auch Runen verwenden und komme mit 0-9 wieder auf genug Zeichen für mein 32’er System. Oder ich nehme nur die Runen und verwende die 24 als Basis. Was dabei raus kommt? Kryptische Zeichen auf dem Bildschirm, wie in der Matrix. Man nehme einfach mal statt 0-9 die Zahlzeichen aus anderen Kulturen:
Auch erfundene Zahlensysteme sind also kein Hexenwerk. Jeder kann sich sein eigenes System ausdenken. Ihr wollt ein eigenes System für eure eigene kleine Fantasie-Welt? Oder eine eigene Alien-Rasse entwerfen die auf ihre eigene Art zählt? Kleiner Tipp: die Aliens in dem Film „Avatar“ (die Na’vi) zählen im octalen Zahlensystem.
Zurück zu Erde
Zu abgehoben geworden? Nun, was das alles mit uns und unserem Alltag zu tun hat ist einfach: Das die Na’vi in Avatar octal zählen macht deswegen Sinn, weil sie an jeder Hand vier Finger haben. Und jetzt wissen wir vermutlich auch warum wir Erdlinge im Dezimalsystem zählen … 😉
Wer so ein Zahlensystem mit der Basis 32 mal ausprobieren möchte kann das unter Tools: Zahlen tun. Dort findet sich auch das duale, das octale und das römische Zahlensystem.
- 2017 in römischen Ziffern? MMXVII.
- 2017 Dual: 11111100001
- 2017 Octal: 3741
- 2017 Hexadezimal: 7E1
- 2017 Base32: 1V1
Lust bekommen?
Viel Spaß beim ausprobieren!